|
| |
| |
| |
Huygens, Leibniz and the ‘petit demon’
Agreement and dissension in their mathematical correspondence
James G. O'hara
Introduction
Late in life, on 14 March 1714, Leibniz wrote the following lines to Nicolas Remond [English translation in Loemker 1969, p. 656]: ‘If I have succeeded in arousing men of excellence to cultivate the infinitesimal calculus, this is because I have been able to give some important examples of its usefulness. When I first told Mr. Huygens something about it in my letters, he scorned it; he did not think there was anything mysterious in it until he saw its surprising applications, which led him to study it just before his death’. The intention of this paper is to examine this assertion by looking at three relevant issues in the unfolding correspondence during the last years of Huygens' life.
Following Leibniz's departure from Paris to Hanover in 1676 the intensive intellectual intercourse with Huygens of the previous four years was reduced and it proved difficult to sustain regular correspondence. Huygens' return to the Netherlands in 1681 was followed by a long pause in their correspondence. Neither Leibniz's communication of a mathematical paper entitled ‘Specimen methodi meae de maximis et minimis’, with an accompanying letter on 5 February 1680, [A III, 4, pp. 71-78] nor a later communication in January 1688, in the wake of Huygens' publication of his solution of the isochrone problem, was answered by Huygens. Even when he did finally write, on 8 February 1690 [A III, 4, pp. 368-371], sending a gift of his recently-published tracts Traité de la lumière and Discours de la cause de la pesanteur, a speedy resumption of the correspondence did not ensue. Leibniz had been absent from Hanover for two and a half years and Huygens' package was mislaid and only delivered in late September 1690. Resumption of regular correspondence came finally after Leibniz's return home in mid June 1690. On 25 July he wrote reporting on his Italian tour and expressing a desire to see Huygens' new tracts. The issues discussed in the correspondence during the period beginning in 1690 were many, complicated and varied. However, three matters discussed in the period in question, lend themselves in particular to test the assertion made by Leibniz to Remond in 1714. These are the discussions concerning and disputes about the so-called ‘Leibniz series’ for the arithmetic quadrature of the circle, the solutions of the catenary problem, and the proposed exchange of inverse-tangent methods between Leibniz and Huygens' collaborator, the Swiss mathematician Nicolas Fatio de Duillier.
| |
The ‘Leibniz series’
The review of Huygens' twin tracts on light and gravity of 1690 in the Acta eruditorum of Leipzig in October and November 1690 produced the first turbulence in the
| |
| |
resumed correspondence between Huygens and Leibniz. In a letter of 9 October [O.C., vol. 9, pp. 496-499; A III, 4, pp. 584-587] Huygens expressed displeasure at the failure of the editors to provide a review of his book. Further contention was brewing in Leibniz's reading of the work. On page 174 of the Discours Huygens had introduced the infinite series
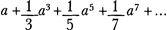
for the quadrature of the hyperbola and commented on the similarity with the Leibniz series for the arithmetic quadrature of the circle published in 1682, viz.
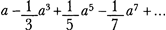
Writing to Huygens on 7 November [O.C., vol. 9, pp. 532-535; A III, 4, p. 640-647], Leibniz remarked that Huygens' series likewise resulted from considerations of his on movement in resisting media published in the Acta in January 1689. He had even employed it in a then unpublished manuscript of 1676 entitled De quadratura arithmetica. Huygens, as we learn from his reply of 18 November [O.C., vol. 9, pp. 536-540; A III, 4, pp. 654-658], was unable to understand the derivation of the quadrature of the hyperbola from Leibniz's series. He rejected any previous knowledge of Leibniz's 1676 paper which, he suggested, Leibniz ought to have published. Leibniz answered in haste, on 24 November [O.C., vol. 9, pp. 546-552; A III, 4, pp. 659-669], to counter any suspicion of conceit on his part in the implication of his previous letter that Huygens had somehow derived his series from the paper on movement in resisting media. With the publication of the eagerly awaited review of Huygens' book a further difficulty arose. The reviewer, Leibniz explains in the same letter, had likewise confused the two series but he denied any hand in this misrepresentation.
When Huygens wrote again on 19 December [O.C., vol. 9, pp. 568-572; A III, 4, pp. 682-691], he still had not seen the review but he requested Leibniz to take steps to have the reported error corrected. He was overwhelmed by what he interpreted as an excuse or apology on the part of Leibniz. Replying on 6 February 1691 [O.C., vol. 10, pp. 9-17], Leibniz expressed astonishment at the suspicion behind Huygens' allusion to an excuse or apology on his part. There was in his view nothing to be excused as he had had no part whatsoever in the misrepresentation. However, knowing Huygens as well as he did, he was prepared to exonerate him. As an alibi he could present a letter of 7 November from Otto Mencke, editor of the Acta, from which he first learned of the review and which was then already in print. Besides, Leibniz suggests, their applications of the series were so different as to rule out any suspicion of plagiarism. Huygens, on 23 February 1691 [O.C., vol. 10, pp. 17-22], now clarified his intentions in alluding to an excuse or apology from Leibniz. Such an apology was of course superfluous as he never had the faintest suspicion of Leibniz's involvement in the affair. Finally, on 2 March 1691 [O.C., vol. 10, pp. 49-52], Leibniz announced that he had written to the Acta to correct the error and clarify the matter and, with the appearance of Leibniz's note on the matter in the April number of the journal, this dispute was finally laid to rest.
| |
| |
| |
The catenary problem
During the four years together in Paris Leibniz had provided Huygens with a preview of his methods in the area of analysis. However Huygens was then, and continued to be later, sceptical concerning the power and superiority of Leibniz's analytical methods over his own geometrical methods. This is particularly evident in their discussion of the catenary problem in 1690 and 1691. On 9 October 1690 Huygens suggested [O.C., vol. 9, pp. 496-499; A III, 4, pp. 584-587] the mathematical description of the catenary - the curve formed by a heavy uniform string suspended from two points of support - as a test for the power of Leibniz's calculus. The problem had previously been posed by Jacob Bernoulli in the Acta eruditorum in May 1690 as a challenge to Leibniz and he had reacted in the July number by setting the term of a year within which other mathematicians might also submit their solutions. Huygens now communicated to Leibniz an encoded solution of the problem and requested the same in return. Replying on 13 October [O.C., vol. 9, pp. 516-520; A III, 4, pp. 619-624], Leibniz announced that he had obtained close agreement with the results expressed in Huygens' anagram, the only difference being an opposite sign in one of his equations. He had determined a number of features and properties of the curve, of its surface of revolution, and of the area between the curve and its axis. On the 18 November Huygens replied [O.C., vol. 9, pp. 536-540; A III, 4, pp. 654-658] that the difference in sign observed by Leibniz appeared to indicate a difference of approach and once again he requested an enciphered solution from Leibniz. The latter, however, failed to comply with this request and the matter rested until early in the new year.
On 23 February 1691 Huygens urged Leibniz [O.C., vol. 10, pp. 17-22] to conclude his work on the catenary so that the results might be communicated to the journal. In his view, the task did not appear to be particularly difficult, unless Leibniz was expecting more than he had obtained himself. On 2 March Leibniz announced to Huygens [O.C., vol. 10, pp. 49-52] that Johann Bernoulli had likewise found a solution whereas their mutual rival Ehrenfried Walter von Tschirnhaus had failed to respond to the challenge. Bernoulli, Leibniz thought, might have profited from his calculus since this, or an equivalent method, would surely be required for the solution of the problem - a remark that conveyed to Huygens the impression that Leibniz had some knowledge of Bernoulli's solution in advance of submitting his own.
Once again, on 26 March, Huygens demanded [O.C., vol. 10, pp. 55-58] that they exchange their results in encoded form in advance of submission. He included a revised version of his own anagram which he suggested might also be offered to Bernoulli in exchange for his. Ignoring Huygens request, Leibniz replied on 20 April [O.C., vol. 10, pp. 83-85] announcing that the editors of the Acta had written to him. Bernoulli had already submitted his solution and he had informed the editors that a solution from Huygens would also be forthcoming. He considered that there was no need to send Bernoulli the encoded solution and he thought that they ought to submit their respective solutions as quickly as possible as the term set had in the meantime elapsed. He pledged Huygens confidentially. In a letter of 21 April, which crossed with Leibniz's of 20 April, Huygens sent a correction to his encoded solution and stressed [O.C., vol. 10, pp. 86-88] for the last time the
| |
| |
necessity of exchanging results in this form. He also announced that he was taking the precaution of sending his solution to an unnamed friend (in fact Henri Basnage de Beauval, editor of the Histoire des Ouvrages des Scavans). Finally on 5 May, without having received the requested encoded solution, Huygens sent [O.C., vol. 10, pp. 93-94] Leibniz his full solution, sealed and ready for forwarding to Leipzig. Three weeks later, on 27 May, Leibniz announced [O.C., vol. 10, pp. 99-100] to Huygens that he had submitted both their solutions.
A pause of nearly two months now ensued before Leibniz wrote again on 24 July [O.C., vol. 10, pp. 109-112] announcing that he had seen the three solutions printed in the Acta for June. Although he had not found time to make a full comparison, his first examination had revealed good agreement in the heart of the matter. He was looking to Bernoulli to make an exact comparison of the three solutions and since the latter had employed his calculus, he expected a share in the glory of his success too. He then presented Huygens with the detailed results of his own first survey - a preview of his paper ‘De solutionibus problematis catenarii’ in the Acta of September 1691. The catenary is mathematically similar to the hyperbolic cosine and so Leibniz could announce that both Bernoulli and himself had related the problem to the quadrature of the hyperbola, both of them had given the tangents, the length or rectification of the curve as well as its centre of gravity. He himself had provided the centre of gravity of the space generated by rotation of the catenary. All three of them had given tangents and the rectification of the curve. Bernoulli and Huygens had surpassed himself in considering the evolute of the catenary. Leibniz singled out Bernoulli for particular praise. He had done extremely well; two or three years earlier he had been far from expectations of such results. His success came of course through his adoption of the calculus of Leibniz. Nonetheless, Leibniz found Bernoulli's constructions quite different from his own. Whereas Bernoulli has been content to assume the quadrature of the hyperbola, or the rectification of the parabola, he himself had reduced the whole to logarithms which he considered a great simplification.
A further issue was the relation of the catenary to loxodrome or rhombic lines i.e. those on the surface of a sphere making equal oblique angles with the meridians. Leibniz refers Huygens to a paper in the Acta of April 1691, ‘Quadratura arithmetica sectionum conicarum’, in which he had treated such loxodrome or rhombic curves, giving results that he had worked out perhaps 15 years earlier in Paris. His interest in this topic had been revived through the investigation of the catenary. Leibniz also recalled that Bernoulli had treated the loxodrome curve in another paper in the Acta of June 1691, entitled ‘Specimen alterum calculi differentialis’. On that occasion Jacob - not Johann as Leibniz seemed to think - had failed to observe that the loxodrome curve is related to the quadrature of the hyperbola, or to logarithms or to the catenary.
Shortly after receiving Leibniz's communication of 24 July Huygens obtained the June number of the Acta containing the three solutions of the catenary problem and the additional paper of Jacob Bernoulli. Huygens first reaction to the outcome of the competition was favourable as we learn from a letter of 1 September [O.C., vol. 10, pp. 127-134]. He too had found good agreement between all three solutions. If Leibniz had obtained more results than himself, it must indeed be due to the facility of the new calculus. For his own part, he had only found those results
| |
| |
he had set out to find and had not sought the additional results provided by Leibniz and Johann Bernoulli.
Huygens added that he had made his discoveries very early on but he had hitherto been unable to relate the catenary to the quadrature of the hyperbola. He had in effect failed using his own methods and thought that, since Johann Bernoulli had also employed Leibniz's calculus, this must have been central to their success. He therefore requested a short explanation from Leibniz. Shortly after dispatching the letter of 1 September, Huygens discovered the means of reducing the construction of the catenary to the quadrature of the hyperbola which he communicated in a follow-up letter of 4 September [O.C., vol. 10, pp. 139-143]. The complementary tone of the previous letter is now replaced by one of reproach or rebuke. In a postscript he presented his thoughts on remarks in Johann Bernoulli's paper relating to the construction of the catenary based on the quadrature of the hyperbola and the rectification of the parabola. Huygens now suggests that Bernoulli's paper, having been sent to Leipzig in December 1690, could have been communicated to Leibniz, a suspicion reinforced by his reading of a statement in Bernoulli's published paper. Although Leibniz had given him an assurance of having had no prior knowledge of Bernoulli's construction, Huygens considered it possible that he might at least have been privy to the fact that Bernoulli had a construction based on the quadrature of the hyperbola. Furthermore, a remark in Leibniz's letter of 13 October 1690 suggested to him that Leibniz did not have the construction in question at that point. Now Leibniz might have avoided this trouble if he had sent his results in encoded form in advance of publication, as he had been called upon to do a number of times.
Replying on 21 September [O.C., vol. 10, pp. 156-162], Leibniz first greeted the agreement found by Huygens between the three solutions and he readily admitted never having contemplated the evolute of the catenary. He then addressed Huygens' rebuke. The latter, Leibniz suggested, having established the reduction of the catenary to the quadrature of the hyperbola, had rightly supposed that they had obtained their results in a similar way. However, his suspicion had gone too far and had now produced a quarrel or dispute between them. He offered an assurance that the editors of the Acta had handled Bernoulli's paper with confidentiality, not even informing him that this solution was founded on the quadrature of the hyperbola. He did however have an alibi who could provide proof of his independent discovery. His alibi took the form of a letter sent to a friend in Florence - intended is Rudolf Christian von Bodenhausen - in late 1690, the latter replying on 19 January 1691 acknowledging the intelligence. As regards Huygens' calls to send an encoded solution, he had been unable to comply and had considered it unnecessary. Furthermore, Leibniz thought that Huygens had distorted the sense of Johann Bernoulli's statement in the published paper; originally Bernoulli had understood the turn of the year 1690/1691 to be the deadline, after which the solutions, having been submitted by all parties, might be exchanged. He himself had been surprised to learn, on seeing the printed papers, that Bernoulli had reduced the problem to the quadrature of the hyperbola. Although he had no knowledge of how Bernoulli had arrived at this, he suspected that the had benefited from the new calculus.
A further possibility was that the investigation of the loxodrome or rhombic curve might have suggested to Bernoulli the construction of the catenary. Developing ideas of Willibrord Snel, Leibniz had demonstrated in his April 1691 article that rhombic
| |
| |
lines can be constructed as a sum of secants of arcs and that this sum corresponds to the quadrature of the hyperbola. Jacob Bernoulli had treated the loxodrome curve in June and had added a supplement on the catenary. Huygens too, Leibniz recalls, in his solution had referred to the quadrature of a curve depending on the sum of secants of arcs, which he had obtained from tables. Leibniz now inquired about this matter but was careful to stress that his own approach had been different. In the same letter Leibniz hit back at Huygens by suggesting that since he had reduced the catenary to the sum of secants of arcs and since he himself had reduced this sum to logarithms in his April paper, Huygens should have been able to understand the connection between the catenary and the quadrature of the hyperbola.
Leibniz also stressed a number of points arising from the investigation of the catenary which supported the superiority of his calculus, such as exponential expressions or logarithms and their application to the catenary and the transformation of quadratures to those of hyperbola and circle.
When Huygens replied after a delay of almost two months, on 16 November [O.C., vol. 10, pp. 182-191], the tone of his letter was again conciliatory. He desired to learn how the new calculus had served Leibniz in obtaining the quadrature of the hyperbola from the catenary. He urged Leibniz to publish this example of the power of the calculus and promised that, if he himself should find something different in his method, he would be willing to publish it too. As regards the doubts expressed in his previous letter, he was now entirely satisfied by Leibniz's explanation. At first he had been taken aback by the words quarrel or dispute and the suggestion that he had distorted the sense of Bernoulli's words. He had acted in good faith and the slight doubt that remained was of too little importance to warrant the use of such expressions in rejecting it.
In the meantime he had examined the work of Snel of 1624, which had provided the inspiration for Leibniz's approach to the loxodrome, and seen how Snel had demonstrated that longitudes could be obtained as a sum of secants. Following a method given by James Gregory in 1668, he himself had found the construction of the catenary and, in his view, more simply than by Leibniz's analysis of the loxodrome which he had not understood at the time of publication. Drawing on a paper commenced in October/November 1690 [O.C., vol. 10, pp. 192-194], he communicated his method of finding the sum of secants to comply with Leibniz's request. Once again he urged Leibniz to make his analysis of curves available, even if the methods, such as the reduction of quadratures to those of circle and hyperbola, had yet to be perfected.
| |
The ‘methodus tangentium inversa’
The third issue on which contention between Leibniz and Huygens developed, concerned Leibniz's ‘methodus tangentium inversa’ - a cornerstone of the calculus by which the construction of tangents was related to the finding of quadratures - and a rival method used by Nicholas Fatio de Duillier, a young Swiss mathematician who collaborated with Huygens and Newton.
In resuming the interrupted correspondence on 25 July 1690 [O.C., vol. 9, pp.
| |
| |
448-452; A III, 4, pp. 532-538] Leibniz sought to outline for Huygens the advantages of his calculus, referring to his fundamental papers in the Acta eruditorum that had appeared in the decade since their previous correspondence. Taking the example of the cycloid he attempted to show how the properties of transcendental curves might be simply described. This led Huygens to formulate, in his reply of 24 August [O.C., vol. 9, pp. 470-473; A III, 4, pp. 545-550], two examples to test Leibniz's ‘methodus tangentium inversa’. In late September and October 1690, Leibniz worked on a paper in which he attempted to solve these problems, employing exponential equations for the solution of the second problem in particular. In a series of drafts for an intended letter [O.C., vol. 9, pp. 521-527; A III, 4, pp. 588-619] Leibniz struggled for the best means of communicating his results to Huygens. Though not yet perfected, Leibniz considered his method adequate for the solution of the problems proposed, depending only on the quadrature of the hyperbola or logarithms.
On reception of a further letter of 9 October from Huygens [O.C., vol. 9, pp. 496-499; A III, 4, pp. 584-587] Leibniz laid this intended letter aside and composed a reply on 13 October [O.C., vol. 9, pp. 516-520; A III, 4, pp. 619-624] in which he communicated his equation for the second of the inverse tangent problems - a transcendental exponential equation that could also be expressed as a differential equation. A follow-up letter of 7 November [O.C., vol. 9, pp. 532-535; A III, 4, pp. 640-647] provided further elaboration of this result. Notwithstanding Leibniz's efforts, the entire question of transcendental equations still seemed obscure to Huygens, as we learn from his reply of 18 November [O.C., vol. 9, pp. 536-540; A III, 4, pp. 654-658]. In two subsequent letters from Leibniz, on 24 November [O.C., vol. 9, pp. 546-552; A III, 4, pp. 659-669] and 5 December [O.C., vol. 9, pp. 555-559; A III, 4, pp. 670-675] respectively, further discussion of the two inverse tangent problems is found. It now became apparent that Leibniz and Huygens were following different conventions regarding signs in the subtangents leading to quite different solutions. On 19 December [O.C., vol. 10, pp. 568-572; A III, 4, pp. 682-691] Huygens admitted a certain admiration for Leibniz's solution. He remained sceptical, however, that a universal rule might exist and he recalled an inverse tangent rule communicated to him in 1687 by Fatio de Duillier that he had not yet properly investigated.
The discussion of the inverse tangent problems continued in early 1691. On 6 February Leibniz maintained [O.C., vol. 10, pp. 9-17] that he had provided the solution of Huygens' problems not as a sign of the perfection of his method but rather of its utility. He considered his exponential expressions to be the most perfect method of representing transcendental curves, since they provided a finite equation containing only ordinary magnitudes in the exponents, and to be at all events superior to serial or differential forms of expression. Leibniz also enquired about Fatio's inverse tangent rule alluded to by Huygens. From the latter's reply on 23 February [O.C., vol. 10, pp. 17-22] Leibniz now learned that Fatio was staying at the Hague. Huygens explained that, whereas he had meanwhile examined Fatio's communication of 1687, Fatio himself had further developed the method and had succeeded in finding the two curves corresponding to the two subtangents proposed by Huygens to Leibniz. However, Fatio was as yet unable to handle cases having roots that contain unknowns and more than a single term.
Leibniz's interest in Fatio's method was now awakened. On 2 March [O.C., vol.
| |
| |
10, pp. 49-52] he disclosed that the little he had seen of Fatio's work had impressed him. As Fatio had found Huygens' curves he had most likely developed short cuts in his calculus. Leibniz now proposed that if Fatio were to disclose his method for the solution of Huygens' problems, he for his part would send his method applied to cases where Fatio had encountered difficulties. On 26 March Huygens announced [O.C., vol. 10, pp. 55-58] that he had proposed the exchange of methods to Fatio. The latter had reservations, however, and still hoped to master the outstanding difficulties with roots and he was accordingly reluctant to send Leibniz what would be a rather lengthy treatise on the subject.
On 21 April, Huygens announced [O.C., vol. 10, pp. 86-88] the intensification of cooperation with Fatio. The latter had confided his inverse tangent method to him and they were developing the method from day to day. It remained to be seen, he tells, if Fatio would find the means of handling composite roots in the subtangent, in which area Leibniz had made such progress.
By early May 1691 Fatio was beginning to see the exchange of papers with Leibniz as a worthwhile proposition. On the fifth of the month Huygens explained [O.C., vol. 10, pp. 93-94] that Fatio had encountered unexpected difficulties in applying his method to cases of subtangents having composite roots and therefore had agreed to the proposed exchange. Huygens gave an undertaking that Fatio's method would be dispatched at once on receipt of Leibniz's method. On 27 May Leibniz agreed [O.C., vol. 10, pp. 99-100] to the exchange and promised to send his paper as soon as official duties allowed. The correspondence between Huygens and Leibniz in the summer of 1691 was dominated by discussion of the catenary solutions. However, a reminder by Huygens on 1 September [O.C., vol. 10, pp. 127-134] of the agreement made with Fatio led Leibniz to suggest a mutual acquaintance, the theologian Gerhard Meier of Bremen, as an intermediary to receive their respective contributions. Leibniz then composed the paper ‘Methodus, qua innumerarum linearum constructio ex data proprietate tangentium...exhibetur’ [O.C., vol. 10, pp. 197-202] which was sent on 5 October to Meier.
On 16 November Huygens wrote [O.C., vol. 10, pp. 182-191] that he had been expecting Leibniz's method for some time and was now grieved that Leibniz was taking precautions as if he might not keep his word. He rejected out of hand the idea of exchanging the papers through Meier and called on Leibniz to fulfill his side of the agreement by sending his paper directly to him. Four days later, on 20 November [O.C., vol. 10, pp. 196-197], Meier forwarded Leibniz's paper.
In this work, following an introductory treatment of the fundamentals of analysis, Leibniz turned his attention to the ‘methodus tangentium inversa’ and stresses the ease with which the problem of inverse tangents could be reduced to quadratures. This is followed by an introduction to his infinitesimal calculus. The renowned Fatio, he explains, had failed in the application of his method when irrationals enter the equation of the subtangent, recalling in particular the example of the subtangent proposed by Huygens. A discussion of the nature of infinitesimals is then followed by an explanation of the terminology of the differential calculus. This calculus, Leibniz asserts, would be the key to the representation of transcendental curves by finite equations. Taking the cycloid as an example he obtained the tangent to this curve and asserted that all the properties of the cycloid could be obtained
| |
| |
analytically from such a calculation. Turning to the example given by Huygens, he obtained the general value of the subtangent and the differential equation allowing the conversion of the problem of inverse tangents to quadratures. This is followed by further illustrations of this reduction to the quadratures of the circle and hyperbola.
In December 1691 Huygens devoted himself to the study of the inverse tangent method of Leibniz and he wrote the paper ‘Methodus Leibnitii’ [O.C., vol. 20, pp. 542-546]. On 18 December he provided Fatio [O.C., vol. 10, pp. 209-212] with a report on Leibniz's ‘Methodus’ before replying to Leibniz [O.C., vol. 10, pp. 221-225] on 1 January 1692.
Huygens' judgement on the merits of Leibniz's paper was harsh. He confessed a lack of familiarity with Leibniz's calculus and admitted that he had wrestled with the paper before getting to the bottom of the matter. His conviction was that in reducing the inverse tangent problem to quadratures Leibniz's method failed to provide the expected advantages. Testing the method on known curves by assuming only a knowledge of their tangents, he found himself always confronted with impossible quadratures. The method failed to reveal whether a curve examined was geometrical or not, and whether or not it required quadratures such as that of the hyperbola for its construction. One would not achieve anything if one was not able to obtain quadratures when possible or at least know when they were impossible. All this combined with Leibniz's assertion that this was the best method at his disposal, led Huygens to suggest that only a small sample of the method had been communicated. In the case of Fatio's method this would not be possible, for the method was such that to reveal a part would be tantamount to revealing the whole. Leibniz ought therefore, he suggests, to resolve to send the principal part of his method.
Replying on 8 January 1692, Leibniz began by having recourse [O.C., vol. 10, pp. 225-230] to a metaphor of an evil spirit - ‘quelque esprit malin’ - to which Huygens later added the words ‘petit demon’, who constantly managed to cause contention between then. Leibniz maintained that he chose to laugh at the malice of this demon. He hoped Huygens had not passed on his paper to Fatio as he now desired to cancel the agreement made. Although under the circumstances Huygens would have the advantage of being privy to both methods, the damage would be limited. He would let it to Huygens' discretion to decide whether he should send something in exchange, but at all events he preferred not to be under obligation to others and the subject of complaint. He remained convinced that he had fulfilled his part of the agreement, for he could say in good faith that to resolve the problem he needed only the means explained in his paper, namely the reduction of the problem to a self-evident quadrature without resorting to a particular method of quadratures. He readily admitted that his method had its limitations but he had understood that the same applied for Fatio's method.
As to Huygens' suggestion that it would be unjust to reveal all of Fatio's method in exchange for only a part of his, he suggested that that part might possibly be of greater value than Fatio's method in its entirety. His own method succeeded, he suggested, in a multitude of cases including those involving transcendental quantities where neither Fatio's method, nor any other given to that time, had succeeded. His infinitesimal calculus, Leibniz was convinced, was superior to that of Archimedes in the same way that the geometry of Viete and Descartes had superseded that of Euclid and Apollonius.
| |
| |
On 4 February 1692 Huygens confirmed [O.C., vol. 10, pp. 238-240] that he had not shown Leibniz's paper to Fatio. He continued to insist that Leibniz had provided only a part of his method, finding it applicable only in cases where the inverse tangent problem had been reduced to the quadrature of the circle or that of the hyperbola. A further defect of Leibniz's method, as he saw it, was that it frequently related the problem to impossible quadratures, even though the curve considered might be simply geometrical. Nevertheless, he offered to communicate some discovery of his, if there was something Leibniz might care to have, in order not to be under obligation to him. Just as Leibniz believed he would be unlikely to profit much from an insight into Fatio's method, so Fatio for his part appeared not to greatly desire Leibniz's method. Fatio claimed to be able to find the equation of the curve in a multitude of cases from the given property of the tangent with composite incommensurables, and he had successfully completed the task for the subtangent given by Huygens without recourse to quadratures. Finally, Huygens himself had doubts about Leibniz's claims concerning the power of his calculus, in particular in investigations relating to the cycloid.
The dispute was laid to rest in the Spring of 1692. Complying with the desire of Fatio [cf. O.C., vol. 10, p. 259], Huygens wrote to Leibniz on 15 March [O.C., vol. 10, pp. 268-270] that Fatio wished that he should reveal his method to Leibniz if he should still be interested. The offer was politely declined by Leibniz on 11 April [O.C., vol. 10, pp. 283-286].
| |
Conclusion
A survey of the correspondence of Huygens and Leibniz from 1690, particularly in relation to the three mathematical issues or disputes considered, appears to collaborate Leibniz's later assertion that Huygens at first threw scorn on his infinitesimal calculus. More generally, in the unfolding correspondence we find that human character traits are revealed which represent important aspects of their respective biographies. Very tentatively it might be argued that, in elaboration and discussion of their respective systems in mathematics, physics and cosmology, friendship and suspicion, a sense of ‘esprit de corps’ within the commonwealth of learning and rivalry, magnanimity and vanity, mutual attraction and antagonism, charm and strangeness enter the close personal relationship of Leibniz and Huygens, his former mentor of the Parisian years (1672-1676). This thesis ought to be tested by a comprehensive examination and evaluation of all the issues arising in the correspondence.
| |
Abbreviations and References
A = G.W. Leibniz, Sämtliche Schriften und Briefe. Berlin, 1923 - (in progress), in seven series). The number of the series is shown in roman numerals, the volume and page numbers in arabic numerals.
Loemker = Gottfried Wilhelm Leibniz: Philosophical Papers and Letters. A selection translated and edited with an Introduction by Leroy E. Loemker. Dordrecht, 1969 (second edition). |
|