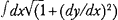De Zeventiende Eeuw. Jaargang 12
(1996)– [tijdschrift] Zeventiende Eeuw, De–
[pagina 215]
| |
Huygens and Newton on Curvature and its applications to Dynamics
| |
[pagina 216]
| |
motion) which Newton investigated was the cycloid pendulum,Ga naar eind9.Ga naar eind10. and he solved it by applying essentially the same physical assumptions and mathematical techniques used by Huygens. Indeed, the further refinement of these techniques led Newton to his first method to calculate the orbits of bodies moving under the action of arbitrary central forces and to the explanation of the physical origin of Kepler's laws of planetary motion.Ga naar eind7. | |
The cycloidal pendulum and the concept of curvatureOne of the great mathematical achievements of Christiaan Huygens was his development in 1659 of the theory of evolutes or curvatureGa naar eind11., evidently motivated by his discovery that the cycloid is the isochronous path for a pendulum weight.Ga naar eind12.Ga naar eind13.Ga naar eind14. Contrary to Galileo's claims,Ga naar eind15. Mersenne had observed that the period of a simple pendulum depends on the amplitude of the oscillations. This dependence led to inaccuracies in Huygens's earliest pendulum clocks which he attempted to correct by installing bend metal strips or cheeks, as he called them, to shorten the effective length of the pendulum for increasing amplitude of the swing (see Figures 1 and 2). The shape of these cheeks were adjusted empirically by requiring the period of the pendulum to be independent of the maximum amplitude, constraining the path of the pendulum weight along a noncircular path.Ga naar eind16. Moreover, applying the relation that the change in the square of the velocity v of a body, falling under the action of gravity, is proportional to the change in its vertical height h, i.e. v2αh for zero initial velocity, called later the principle of energy conservation,Ga naar eind17. Huygens carried out a remarkable calculation for the period of the pendulum oscillations for small amplitudes. Exploring the approximations which he had made in this calculation, he found that his result for the period would apply also for arbitrary amplitudes if the path of the pendulum weight was a cycloid.Ga naar eind18.Ga naar eind19. Excited about his discovery, he promptly communicated this result to his former mathematics teacher, Frans van Schooten,Ga naar eind20. and to some of his friends, without giving any proofs until 14 years laterGa naar eind21. with the publication of the Horologium Oscillatorium. During this intervening period, Huygens' problem, to find a proof for the isochronous property of the cycloid path of a pendulum weight, posed one of the most difficult challenges in mathematical physics to his contemporaries. One need only read the repeated false starts made by Lord Brouncker,Ga naar eind22. then President of the Royal Society, to appreciate the mathematical skill and physical insight exhibited by Huygens in solving this problem.Ga naar eind23. Eventually the brilliant French Jesuit Ignacius Gaston Pardies found an elegant scaling proof for the isochronous property of the cycloidal pendulum,Ga naar eind24. and Newton was able to obtain a complete solution to this problemGa naar eind25. including the analytic expression for the period of the pendulum as well as a demonstration that the evolute of a cycloid is a similar cycloid.Ga naar eind10. There is no evidence that Huygens responded to Newton's 1673 letter quoted above, in which he had offered to send him his method of solution. However, contrary to some views,Ga naar eind26. Newton's solved this problem by virtually the same mathematical techniques that Huygens had used in 1659, and therefore it is unlikely that Huygens would have learned anything new from him. This is not surprising, because Newton learned many of the contemporary mathematical methods of | |
[pagina 217]
| |

1. An early sketch by Huygens showing the path KGEL of a weight oscillating a the end of a string HG. This is intercepted at points F and B corresponding to a polygonal cheek HFB. (O.C., vol. 17, p. 17)
calculus by reading Descartes' Géométrie in the second edition (1659)Ga naar eind27. translated from the Latin by Frans van Schooten,Ga naar eind28. who had been Huygens's private tutor and professor of mathematics at the University of Leiden. In this translation, van Schooten wrote extensive commentaries, and included new results obtained by Huygens and by some of his other gifted students Jan Hudde, Hendrik van Heuraet and Jan de Witt. In 1653 Huygens had solved Apollonius' problem of determining the normals to a parabola from a given point by applying Descartes' algebraic geometry to construct and solve graphically a cubic equation (see Fig. 3). At the end of his short paper he pointed out that, depending on the location of this point, there were three possible cases corresponding to the existence of one, two or three normals. The condition for the existence of only two normals to the parabola from a fixed point determines a curve which separates the plane into a domain where there is only a single normal from another domain where there are three normals. This curve corresponds to the evolute of the parabola, but it was not given in this paper. In his original Géométrie (1637), Descartes had used the tangency of a circle to a given point on a curve to obtain the normal to the curve at that point, but apparently the connection of normals to tangent circles was not considered by Huygens at this time. However, a year later Huygens called van Schooten's attention to a special case of the general solution of the intersections of a circle with a parabola,Ga naar eind29. which van Schooten had discussed in a commentary to the third book of Descartes' Géométrie in the first edition (1649) of his Latin translation | |
[pagina 218]
| |

2. A picture of Olaf Romer at his transit instrument (from P. Horrebow's Basis Astronomiae ..., Ch. VIII. Copenhagen, 1735) showing on the left side his indispensable Huygens' pendulum clock. Romer's 1676 discovery of a delay in arrival on the earth of the light signals coming from the eclipse of Io, a moon of Jupiter, was made possible by the accuracy of one of Huygens' clocks.
of this work.Ga naar eind30. In this commentary, van Schooten had given the parameters of this circle in terms of the coordinates of three adjacent intersections (see Fig. 4), and Huygens emphasized the special case when these intersections coalesce at a single point.Ga naar eind29. Huygens called special attention to the interesting fact that in this case the circle cuts the parabola while it has a common tangent with the parabola | |
[pagina 219]
| |

3. This page from Huygens' notebook, dated 17 September 1653, shows three graphical evaluations of the normals to a parabola from a fixed point labelled C. Huygens' method to obtain the figures is described in n. 31. The figure on the left hand side and in the middle show a single normal from C to a point A on the parabola, while the right hand figure shows three normals from C. A case for only two normals is not shown, although the existence of this special case is indicated in the text. To find the locus of the points C for this case requires an analytic argument (coalescence of two adjacent normals) which is not presented in the manuscript (Leiden University Library, ms Huyg. 12, f. 122; O.C., vol. 12, pp. 81-82.
at the intersection point (see Fig. 3).Ga naar eind31. This time it may not have escaped Huygens' attention that this limit corresponds to his previous solution when two of the three possible normals from a fixed point to a parabola coalesce. This case determines the center and radius of the osculating circle to the parabola, as Leibniz was to name it 32 years later.Ga naar eind32. As had been pointed out by Descartes in his Géometrie, the coincidence of two intersections of a circle and a parabola determines a tangent circle, that is, at the intersection this circle and the parabola have a common tangent. Then if the radius of this circle is varied until a third intersection coincides with the first two, the center of this circle is also the intersection of two coalescing | |
[pagina 220]
| |

4. A page of the second edition of van Schooten's Latin translation of Descartes' Géométrie showing the diagram for the intersections of a circle and a parabola, and the insertion (on top of p. 339) of Huygens' condition for an osculating circle.
normals to the parabola. Van Schooten promptly included Huygens' results in his extended commentaries of the second edition (1659) of his book (see Fig. 4).Ga naar eind33. Newton, who in 1664 began his studies of tangents and curvature by reading this edition,Ga naar eind34. would have paid special attention to these results.Ga naar eind35. Another important result included in van Schooten's book was Hudde's method to evaluate double and higher order roots of algebraic equations. Indeed, one of Newton's techniques to obtain the osculating circle, was to apply Hudde's method to obtain the triple roots of the quartic equation for the intersection of a circle with a parabola.Ga naar eind35.Ga naar eind36. In solving Huygens's challenging cycloid pendulum problem, both PardiesGa naar eind24. and NewtonGa naar eind37. considered a fundamental physical question which seems to have been overlooked by Huygens at that time, and was not discussed in his Horologium Oscillatorium. The question concerns the underlying reason for the isochronous property of the oscillations of a body moving on a cycloidal path under the action of the constant force of gravity. They found that the component of the force of gravity tangent to a cycloidal path is proportional to the distance along this path.Ga naar eind38. This result implies that other physical systems where the force is linear with the distance leads to isochronous or harmonic oscillations. The best known example is the restoring force of a spring. This property of springs was first pointed out by Pardies,Ga naar eind24. and later by HuygensGa naar eind39. who was apparently aware of Pardies' work, and | |
[pagina 221]
| |
also by Robert HookeGa naar eind40. (it is now known as Hooke's law). Both Huygens and Hooke applied this property to develop a spring balance to regulate a clock as a substitute for the pendulum, and presumably for this reason Huygens withheld his result from publication, while Hooke delayed writing his account. Thus, the discovery of one of our most fruitful results in physics, harmonic oscillations, appeared first through the study of Huygens' cycloid pendulum (an early example of applied research leading to fundamental physics). After discovering mathematically that the cycloid is the isochronous path of a weight moving under the action of gravity, Huygens proceeded to study, also mathematically, the shape of the cheeks restricting a weight suspended by a string to move along this curve. This study led him to develop further mathematical methods to obtain the evolute or center of curvature of a given curve. The evolute corresponds precisely to the curve for the cheeks which restricted the motion of the pendulum weight on a given path.Ga naar eind16. For the cycloidal path, he found that its evolute is a similar cycloid.Ga naar eind14. Seven years later, unaware of Huygens' result, Newton also developed the theory of evolutes along precisely the same lines. Given a curve, which Huygens calls the evolute, he considered another curve now called the evolvent or involute which is described, in his own words, as follows: ‘If a string or flexible line is understood to be stretched around a curve in one direction, and if one end of the string remains fixed while the other end is pulled away such that the freed part of the line always remains taut, then it is clear that some other curve is described by this end of the string. This latter is called the curve “described by evolution.”’Ga naar eind2. The mechanical origin of this definition, based on the construction of a pendulum with cheeks, is further in evidence as he continues: ‘The curve around which the string has been stretched is called the evolute.’Ga naar eind2. Since the length of the string at a given point on the evolute is equal to the corresponding arc length of this curve, to obtain the evolvent requires the length of an arc (rectification) of the evolute, which is a problem of integration.Ga naar eind41. However, in Proposition 1 of the Horologium Oscillatorium, Huygens proves that ‘Every straight line tangent to an evolute meets a line described by evolution at right angles.’ Hence Huygens considered the problem of obtaining the evolute given an evolvent by finding the envelope of the lines perpendicular to the evolvent. A point on the evolute is obtained by considering the intersection of two adjacent lines each of which is perpendicular to the evolvent in the limit that these lines approach each other. The length of the limit line corresponds to the radius of curvature of the evolvent, although the term curvature was not used by Huygens in his book.Ga naar eind11.Ga naar eind32. Huygens' construction, given in Proposition 11 corresponds precisely to one of the methods developed by Newton in 1664 to determined the curvature or evolute of a parabola and of several other curves.Ga naar eind42. In subsequent years, Newton extended his technique further, and by 1671 he even obtained the evolute of a curve in polar coordinates.Ga naar eind43. In his tract on methods of series and fluxions problem 5, to find the curvature of any curve at a given point, begins with ‘the problem has the mark of | |
[pagina 222]
| |
exceptional elegance and of being pre-eminently useful in the science of curves’. Moreover, the geometrical and algebraic calculus techniques developed by Newton to evaluate the evolute were virtually identical to those of Huygens. In describing his results for the evolute of a parabola, Newton states ‘... note that the crooked line [evolute] ... is always touched by the perpendicular line [to the evolvent] in such sort as to be measured by it ... By this means the length of as many crooked lines may be found as desired ...’,Ga naar eind44. which echoes Huygens' formulation quoted above, although Newton could not have seen Huygens's great work at that time. | |
De Vi CentrifugaIn dealing with the dynamics of the pendulum, Huygens was led to consider the force or tension restricting a body to circular motion. For uniform velocity v (in the absence of external forces) he obtained the celebrated result that this force, which he named centrifugal force, is proportional to the acceleration a,
where ρ is the radius of the circle. Although Huygens had obtained this result already in 1659, an announcement of this result first appeared at the end of the 1673 Horologium Oscillatorium, and his calculations and proofs where published only posthumously in 1704 in the Vi Centrifuga.Ga naar eind45. Newton's Waste Book reveals that by 1664 he had also found the same relation, Eq. 1.Ga naar eind46. It is interesting that for one of the first application of this result, both consider the effect of the rotation of the earth on the net gravitational attraction at the equator. Since ancient times the main argument against the rotation of the earth as an explanation of the apparent daily rotation of the sun and the stars had been that objects would then fly off its surface. Galileo had pursued this question earlier, but gave an incorrect solution. Applying Eq. 1 with ρ equal to the radius of the earth, and v = 2πρ/T, where T is the period of rotation, HuygensGa naar eind14. calculated for the ratio of gravity to centrifugal acceleration g/a = 280, while NewtonGa naar eind47. obtained the value 350, thus putting finally to rest the objections against the rotation of the earth (the difference in values of g/a was due mainly to different estimates of the radius of the earth). However, Newton went a step further in applying Eq. 1 to obtain also the radial dependence of the gravitational force. From the observation that the period of the planets, which rotate approximately in circular orbits around the sun, obeyed Kepler's third (harmonic) law (that the square of the period varied as the cube of the radius), he could deduce from Eq. 1 that the gravitational force or acceleration must depend on the inverse square of the distance between the sun and a planet. There is no evidence that Huygens also made this crucial deduction which was obtained later by Wren, Hooke and Halley, as acknowledged by Newton in the Scholium to Proposition 4 of Book 1 of the Principia. Huygens considered also the tension or force on the string suspending a pendulum weight due to the combined effect of gravity and motion along a circular | |
[pagina 223]
| |
arc. In particular, if the suspension point for the oscillation of a simple pendulum is abruptly changed by means of an intervening nail, as envisioned originally by Galileo, Huygens found the correct condition (missed by Galileo) for which the pendulum weight would wrap itself around the nail.Ga naar eind48. Although he applied his method to obtain the evolute for several curves including conic sections, there does not appear to be evidence that he considered the corresponding tension for bodies moving on these curves under the action of gravity. While Huygens restricted his dynamical investigations to the motion of bodies constrained (by strings and cheeks) to move along prescribed trajectories under the action of a constant (gravitational) force, as early as 1664 Newton began to consider the unconstrained motion of bodies under the action of central forces. One of his motivations appears to have been to understand Kepler's law that planetary motion occurs along elliptical orbits with the sun at one of the foci. At that time Newton had written in his notebook (Waste book)Ga naar eind49. that ‘If the body b moves in an Ellipsis, then its force in each point (if its motion in that point be given) may be found by a tangent circle of equal crookedness with that point of the Ellipsis.’ As Newton's mathematical papers reveal, the term crookedness was his early expression for curvature, and tangent circle corresponds to the osculating circle found by Huygens earlierGa naar eind30. as named by Leibniz 32 years later. If ρ is the radius of curvature at a given point of an ellipse on which a body moves with varying velocity (motion) v, then the result which he, and independently Huygens, had obtained for circular motion, Eq. 1, applies in this case to the component of the acceleration or force perpendicular to the orbit. For central forces this component is a sin(α), where α is the angle between the tangential and the radial direction, leading to a straightforward generalization of Eq. 1,
Evidently this is the meaning in mathematical form of Newton's cryptic remark. However, there remains the question of determining the velocity v along the ellipse which Newton takes as given. For motion along an ellipse or along any other noncircular orbit this velocity is not a constant because there is also a component of the force or acceleration which is tangential to the orbit, and is given for central forces by a cos(α). This tangential component of the acceleration determines the time rate of change in velocity, dv/dt = acos(α), and therefore the velocity can be evaluated from given initial conditions. Since the radial component of the velocity determines the time rate of change of radial position, dr/dt = - v cos(α), eliminating the time variable gives immediately the relation
This equation is the differential form for central forces of the principle of conservation of energy which both Huygens and Newton originally had applied to solve the dynamics of the pendulum for constant gravitation acceleration, a = g. Newton also applied it to harmonic oscillator motion, where a = cr and c is a constant and | |
[pagina 224]
| |

5. (left) This page from Newton's Waste book, dated February 1664 and entitled ‘The crookedness [curvature] in lines may be otherwise found as in the following examples’, shows at the top of the left hand margin a diagram of an osculating circle intersecting a parabola. The parameters of this circle are evaluated, as described in the text, by solving for the triple root of a quartic polynomial obtained from the intersections of a circle with a parabola. The diagram below shows the four intersections a general circle with a parabola which bears a close resemblance to diagrams in van Schooten's Geometria (see Fig. 4). (By permission of the Syndics of Cambridge University Library; Mathematical Papers (n. 10), vol. 1, pp. 259-262.)
| |
[pagina 225]
| |
later he gave an equivalent geometrical derivation of this principle in Proposition 39, book 1 of the Principia. Given the radial dependence of the central force a, Eq. 3 can be integrated to determine the radial dependence of v2 up to a constant corresponding to the total energy E, where v2/2 = - f adr + E. Substituting this expression for v2 in the centrifugal force relation, Eq. 1, determines the radial dependence of ρsin(α), a purely geometrical quantity, in terms of v2/a which depends only on the dynamics, i.e. the force law and the initial conditions. Orbits satisfying these relations can be easily computed approximately by a straightforward generalization of Huygens' and Newton's method of evolution (see Fig. 5), and there is considerable circumstantial evidence that this method was indeed applied by Newton in his earliest computations of orbital motion for central forces.Ga naar eind7. In this case neither the evolute, which corresponds to the orbital curve, nor the evolvent is known in advanced, but both curves are obtained from the condition that the radius of curvature ρ and the relative angle α between the tangential and radial directions, satisfy Eqs. 2 and 3. Assuming a given curve for orbital motion under the action of central force, Newton could also evaluate the curvature ρ and angle α and then apply Eqs. 2 and 3 to solve for the force. However, in practice only a few simple curves, e.g. conic sections and spirals, provide an analytic solution, while other cases can be solved only approximately.Ga naar eind50. The simplest case is the spiral (equiangular) orbit which Newton first mentioned in his December 13, 1679 letter to Hooke,Ga naar eind7.Ga naar eind51. without however giving the corresponding force law. By 1671 Newton had shown that for such a spiral the quantity ρsin(α) = r. Hence Eq. 2 for the force or acceleration implies that v2 = ar, or in differential form, that dv2/dr = rda/dr + a. Combining this result with the differential form of the principle of energy conservation, Eq. 3, gives rda/dr = - 3a, which implies that ar3 is a constant. Thus, for this spiral orbit the central force or acceleration depends inversely with the cube of the distance. Newton first revealed his remarkable result, without however giving any proof, in a Scholium of his 1684 De Motu,Ga naar eind52. the earliest known draft of some of the fundamental propositions of the Principia. Later a geometrical scaling proof appeared in Proposition 9 of the first book of the Principia. A similar calculation for conic sections leads to Newton's fundamental result that the corresponding force varies inversely as the square of the distance,Ga naar eind53. forming the basis of his theory of gravitation. | |
SummaryHuygens' development of cheeks to construct an isochronous pendulum clock, led him to his method of evolution which determines one curve, the evolvent, by the | |
[pagina 226]
| |
mechanical operation of unwinding a taut string wrapped about another curve, the evolute (cheeks). In Proposition 2, part 3 of the Horologium Oscillatorium he presented a mathematical method for the converse construction: ‘Given a curve line [evolvent], find another curve [evolute] whose evolution describes it ...’ His mathematical procedure, developed also by Newton, was to determine the locus of the intersection points of two adjacent normals to a curve in the limit that these two normals coalesce. This limit corresponds to a special solution of Apollonius's problem, which Huygens had obtained for the parabola in 1653, and again in 1654 for a special limit of the intersection of the parabola with a circle, which he had brought to van Schooten's attention. The dynamics of the pendulum also led him to consider the force or tension on the string, and he obtained the fundamental relation for centrifugal acceleration for circular motion with uniform velocity, Eq. 1. Almost a decade before the publication of Huygens' great work, the Horologium Oscillatorium, Newton followed an analogous path of discovery to develop concepts of curvature and of centrifugal force, applying similar mathematical methods and physical insights to problems that Huygens had solved earlier. This was not a coincidence, but is due in great part to the publication of a translation into Latin of Descartes' Géométrie by Frans van Schooten, a mathematics professor at the University of Leiden. In this book, van Schooten included extensive commentaries and original contributions by some of his students which included Huygens himself. The influence of this book on Newton's early development in mathematics cannot be overestimated.Ga naar eind54. Newton generalized the concept of centrifugal force to non-circular orbits, and the energy conservation principle to arbitrary central forces. This enabled him to obtain, for the first time, the geometrical properties of orbital motion for general central forces and to solve the fundamental problem of celestial mechanics in the seventeenth century concerning the physical origin of Kepler's law of planetary motion. In the first edition (1687) of the Principia, Newton took a different approach to describe orbital dynamics, based on suggestions made in 1679 by Hooke,Ga naar eind7.Ga naar eind55. and his concepts of curvature and of centrifugal force were hidden in some lemma's and corollaries.Ga naar eind56. This has made it quite difficult to see the connection of his major work to Huygens' work and to his own earlier concepts of curvature and centrifugal force. Already by 1687 Newton had applied these principles, although without much explanation, in some of his calculations of the perturbations of the lunar motion by the solar gravitation force, in corollaries of Proposition 66 in book 1, and Proposition 28 in book 3 of the Principia. However, only in the two later editions (1713 and 1726) of the Principia, did Newton apply his approach based on curvature and generalized centrifugal force as an alternate method of solution of his fundamental propositions. For this reason it had been thought that what appears now to be his earliest dynamics 7 represented instead his later more mature dynamics.Ga naar eind57.Ga naar eind58. | |
[pagina 227]
| |
AcknowledgementsI would like to thank H.J.M. Bos and D.T. Whiteside for many useful comments, and my colleagues in the Physics Departments of the University of Leiden and the University of Amsterdam where this work was completed for their kind hospitality. |
|


 (1)
(1)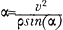 (2)
(2) (3)
(3)